Mentor: Uri Pryadkin

July/August 1995

1 Introduction

Previous mathematicians [Turk and Pentland], have theorized that certain cognitive processes, such as face recognition, can be emulated through the use of principal component analysis. In the project which we have worked on, at the International Summer Science Institute, under the supervision of our mentor Uri Pryadkin, we have attempted to use techniques of principal component analysis, more specifically, eigen-vector analysis, to develop a computer program capable of face recognition. Specifically, the goal of our project was to investigate a mathematical basis and model for face recognition using principal component analysis with eigenvectors, and then implement a working model in the form of a computer program.

The fundamental idea behind principal component analysis with eigenvectors has its basis in linear algebra. Put simply, if there are a series of multi-dimensional vectors representing objects which have similarities, it is possible to use a transformation matrix and eigenvectors to orient a space which requires fewer dimensions to accurately describe these multidimensional vectors. For instance, if in three dimensional space, there was a cloud of particles that lied in a two dimensional plane skewed from the axes (Fig 1), it would be possible to orient a new space with a new origin and new unit vectors such that the cloud which previously required a three dimensional representation could now easily be represented in only two dimensions.

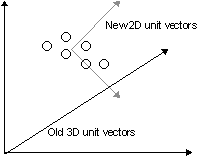
Figure 1: Series of objects in 3D space which can be represented by 2D vectors

The new unit vectors of the lower dimensional space, which now sufficiently describes where the points are located, can be derived by normalizing the eigenvectors of the transformation matrix used to create the new origin. Lower eigenvalues, that is eigenvalues approaching zero, correspond to unit vectors in dimensions which don’t have to be represented. Consequently, the vectors corresponding to these eigenvlaues can be disregarded thus reducing the dimensions of the space even further.

2 Method

2.1 Overview

The task of having computers capable of recognizing faces, without using principal component analysis, is a formidable one. To a computer, a face, like any other image, is a matrix of several hundred pixels by several hundred pixels. Dealing with many faces , in the form of pictures, can be very time consuming and difficult. If, however, one applies principal component analysis, the task becomes much more manageable. If the picture’s pixel matrix is turned into a vector, then that picture will have a location vector in a hundred thousand dimensional space. If the same is done with other pictures, their location vectors will wind up in the same area of this huge multi-dimensional space. We call this small subsection of the multi-dimensional space the "face space." Then using eigenvectors to create a new basis for the representing the images, one can now represent images as coordinates in a much smaller dimensional space. Images of the same person, will, of course, be located nearer to one another in this space, as they are similar to one another. At this level, the task of recognition becomes merely a matter of determining the location of the vector form of a new picture in a lower dimensional space relative to pictures of recognized faces.

2.2 Initialization with Training Set

In order to apply the ideas of ideas of principal component analysis to face recognition, we had to take care of preliminaries. Firstly, the faces being discussed are nine 512*352 pixel 8-bit TIFF images, consisting of three separate images for three separate people, which we converted into vectors of 180,224 dimensions. Our first task was to find an average face, y. This was easily done by taking the arithmetic mean of the face vector.

Figure 2: The "average face"y of our nine sample faces

We then constructed a matrix A, which consisted of the differences between each face and the average face. Then, by creating a coovariance matrix C = A * A’, we can easily find the eigenvectors of C, which by proof [Turk and Pentland, p.6], will span the "face space." The eigenvectors whose corresponding eigenvalues are less than one can be discarded. Then, if the eigen vectors are normalized (ie. divided by their length), they will now, also by proof [ibid], compose the basis of this lesser dimensional space. Also, they will be orthogonal and orthonormal. Now, instead of being a 180,224 byte matrix, the images we used became eight numerical co-ordinates in our new "face space"!

2.3 Recognizing Faces

Once faces can be represented as coordinate vectors in a low dimensional space, the task of face recognition itself is rendered trivial. First we look at the placement of different vectors representing different pictures of the same person. We average these vectors to find the "center" image of this person and then calculate a "radius" from this center to the different images. New pictures are broken down into lower dimensional vectors using simular techniques as used to establish the coordinates of the test faces. Essentially, we make a vector and multiply by the eigenvectors to determine coordinates. Now, face recognition simply becomes the mathematical calculation of distance, to see whether or not a new face falls into a "sphere of recognition" of a previously recognized face.

3 Results

3.1 Using the Algorithm for Face Recognition

We did ... phase1.. This took a few hours to run on a Silicon Graphics, which was running "some" other processes at this time. Here are three of the nine images; theses are of the same person:

Figure 3: Three of the nine images in the training set

mtv, vtm

To recognize an image, we wrote a new function...

Here is another image of that person. After running for some minutes, our program identified him as being the same as the three above.

Figure 4: A new image that our program identified well

3.2 Using the Algorithm for Image Compression

The idea that faces can be represented with only a few "coordinates" and the principal components, which are only stored once, inspired us to use this method for image compression. In fact, [Turk, Pentland, p.5] refer to [Sirovich, Kirby] and state that this algorithm was originally designed for compression!

Here are the results of three experiments that we performed with different images:

1. We took a completely new face of a person that was not in the training set, calculated its (in our example) eight weights describing the position of the face in the "face space" and rebuilt the image using the linear combination of the eight principle components. What comes out is the following:

{figure}

Figure 4: A reconstructed face of a person that was not in the training set

As one can see, the result is very poor. It has to be said that this could probably be improved by using more than eight principle components (eigenfaces). [Turk, Pentland] speaks of using about 40 eigenfaces.

2. In another decomposing/rebuilding experiment, we did the same with an unknown face of a person of whom we have had three different images in the training set. The following figure shows that the result is much better in this case:

{figure}

Figure 5: A reconstructed face of a person that was in the training set (with different faces)

3. As a third experiment, we decomposed/rebuilt the image of a face that was itself part of the initial training set. As one can imagine, the quality of this image was perfect; no difference from the original picture could be seen.

4 Discussion

4.1 Suitability of MATLAB

We were using MATLAB for the realization of our project. Though we had no previous knowledge and expierence with this computer algebra system, we found it very easy to learn and useful for experimenting. Especially calculations invoking matrices and vectors are very simple. Still, it has to be stated that we cannot think of using MATLAB in a real application, say for a security system, because it is far too slow. We would use a C++ program for this purpose; the matrix calculations could be simplified and optimized by using an industry standard math library such as Matrix.h++ from RogueWave Sofware Inc.

4.2 Efficiency of the Algorithm & Suitability for Industry Use

Recognizing faces could theoretically (see previous chapter concerning MATLAB or C++) be very fast, because it consists only of a matrix subtraction, one matrix multiplication and a bit of comparison. On the other hand, training new faces is a comparably complicated calculation, especially if the "face space" has to be recalculated as soon as new persons are added. We would therefore say that this method could be useful in a serious industry application only to recogninze a group of people that does not often change after initial training.

5 Acknowledgments

We want to thank our Mentor Uri Pryadkin and the staff of the Summer Science Institute.

6 References

[1] Matthew Turk, Alex Pentland: Eigenfaces for Recognition; Vision and Modeling Group, The Media Laboratory, Massachusetts Institute of Technology; September 1990.

[2] L. Sirovich and M. Kirby: Low-dimensional procedure for the characterization of human faces; J. Opt. Soc. Am. A, Vol. 4, No. 3, March 1987, 519-524.

[3] M. Kirby and L. Sirovich: Application of the Karhunen-Loeve procedure for the characterization of human faces; IEEE Trans. Pattern Analysis and Machine Intelligence, Vol 12, No. 1, Jan. 1990.

7 Appendix: MATLAB Source Files

see MATLAB scripts (http://www.vorburger.ch/projects/faces/matlab.html)